What is Statistical Learning

In essence, statistical learning refers to a set of approaches to estimate $f$. Let's look it in detail.

We can denote the input variables as $X$. The inputs go by different names, like predictors, independent variables, features, or sometimes just variables. The output variable is often called as dependent variable or response, and it typically denoted as $Y$. We use these input variables to predict output variable, and we call this progress as statistical learning.

More generally, suppose we observed a quantitative response $Y$ and $p$ different predictors, $X_1, X_2, \dots, X_p$. We assume there is some relationship between $Y$ and $X=(X_1, X_2, \dots, X_p)$, which can be written in a very general form $$Y=f(x)+\epsilon.$$

Here $f$ is some fixed but unknown function of $X$, and $\epsilon$ is a random error term, which should be independent of $X$ and has mean zero.

Why Estimate $f$

In many situations, we already have a set of inputs $X$, but the output $Y$ cannot be easily obtained. In this setting, since the error term average zero, we can predict $Y$ using $$\hat{Y}=\hat{f}(X),$$ where $\hat{f}$ represents our estimate for $f$, and $\hat{Y}$ represents the prediction for $Y$.

In general, $\hat{f}$ isn't a perfect estimation of $f$. Then, how to measure the accuracy of our prediction?

The accuracy of $\hat{Y}$ as a prediction of $Y$ depends on two quantities, which we called reducible error and irreducible error. We can improve the accuracy of $\hat{f}$ to reduce the reducible error. However, even if there exists an $\hat{f}$ by using appropriate statistical technologies can perfectly estimate $f$, our prediction will still have error in it! Because $Y$ is also a function of $\epsilon$. This error is irreducible.

Consider a given estimate $\hat{f}$ and a set of predictions $X$, which yields the prediction $\hat{Y}=\hat{f}(X)$. Then it is easy to show that $$\begin{align*} E(Y-\hat{Y})^2 =& E[f(x)+\epsilon-\hat{f}(X)]^2\\ =& \begin{matrix}\underbrace{[f(X)-\hat{f}(X)]^2}\\Reducible \end{matrix} + \begin{matrix} \underbrace{Var(\epsilon)} \\irreducible \end{matrix} \end{align*}$$ What we focus most is on the techniques for estimating $f$ with the aim of minimizing the reducible error. And irreducible error will always provide an upper bound on the accuracy of our prediction for $Y$. And this bound is almost always unknown in practice.

If we are interested in the way how $Y$ is effected with $X_1, X_2, \dots, X_p$ change, we cannot treat $\hat{f}$ as a black box, we need to know the exact form of $\hat{f}$.

How to estimate $f$

Our goal is to apply statistical learning methods to the training data in order to estimate the unknown function $f$. Most statistical learning methods can be charactered as parametric or non-parametric.

Parametric methods

Parametric methods involve a two-step model-based approach.

1. First, we make an assumption about the functional form, or shape of $f$.
2. After a model has been selected, we need a procedure that uses the training data to fit or train the model.

Non-parametric methods

Non-parametric methods do not make explicit assumption of function form of $f$. Instead they seek an estimate of $f$ that gets as close to the data points as possible without being to rough or wiggly.

Since non-parametric methods avoid the assumption of a particular functional form of $f$, they have the potential to accurately fit a wider range of possible shapes for $f$. However, the major disadvantage is it requires a very large number of observations in order to obtain an accurate estimate of $f$

The Trade-off Between Prediction Accuracy and Model Interpretability.

The relationship between flexibility and interpretability is showed as below:

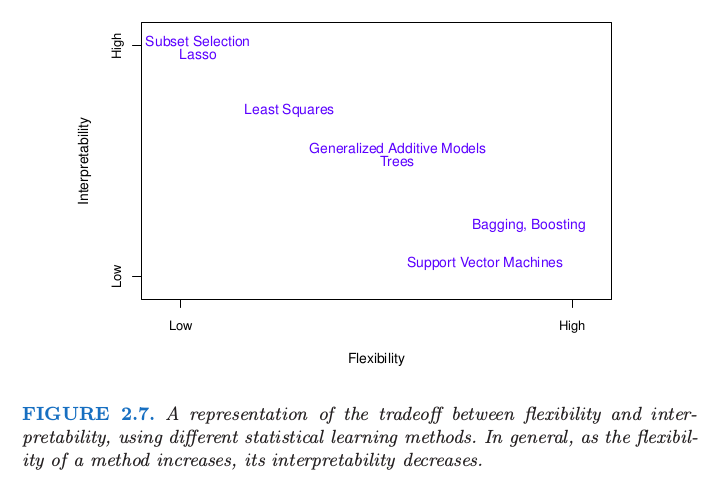
However, we will often obtain more accurate predictions using a less flexible model. It may seem counterintuitive at first glance, but highly flexible model may cause over-fitting.

Supervised versus Unsupervised

Most statistical learning falls into to categories: supervised and unsupervised.

Supervised learning has a response variable $Y$, but unsupervised learning has no response variable $Y$ to supervise our analysis. Cluster analysis is a typical unsupervised learning method.

If the predictor can be measured cheaply but the corresponding response are much more expensive to collect, we refer this setting as a semi-supervised learning problem.

Regression versus Classification

Variables can be characterized as either quantitative or qualitative (also called categorical).

We tend to refer to problems with a quantitative response as regression problems, while those involving a qualitative response are referred to classification.